DSA学习笔记
C++相关
参考Why do I have to access template base class members through the this pointer?,继承模板父类的子类,调用父类成员变量时需要使用 ParentClass<T>::member 或 this->member 的方式,否则msvc2017报 identifier not found 错误。
二叉树
Quiz
-
In the graph implemented with adjacency matrices with n vertices, the vertex v has m neighbors, and the time complexity of traversing all m neighbors is: 在包含n个顶点的用邻接矩阵实现的图中,顶点v有m个邻居,遍历所有m个邻居的时间复杂度为:
A. O(1); B. O(m); C. O(n); D. O(mn);
因为是邻接矩阵实现,空间为O(n*n), 扫描v的邻居需要扫描一行即 O(n)次
-
G is a directed acyclic graph, and (u, v) is an edge in G that points from u to v. The result of DFS on G is: G是有向无环图,(u, v)是G中的一条由u指向v的边。对G进行DFS的结果是:
A. dTime(u) > dTime(v); B. dTime(u) < dTime(v); C. fTime(u) > fTime(v); D. fTime(u) < fTime(v);
有向且无环,无法推出B,因为还可能存在其他指向v的边。只能推出 C. fTime(u) > fTime(v),因为无论如何,必然是v先完成访问达到visited状态。
图
下面的表引用自《离散数学及其应用》。
| 类型 | 边 | 允许多重边 | 允许环 |
|---|---|---|---|
| 简单图 | 无向 | 否 | 否 |
| 多重图 | 无向 | 是 | 否 |
| 伪图 | 无向 | 是 | 是 |
| 简单有向图 | 有向 | 是 | 是 |
| 有向多重图 | 有向 | 是 | 是 |
| 混合图 | 有向的和无向的 | 是 | 是 |
Quiz
-
Q: In a simple undigraph with 20 vertices, the maximum number of edges is ? 在含20个顶点的简单无向图中,边的数量最多为? The degree of the vertex with the smallest degree at this time is ? 此时度最小的顶点的度为 ?
A: 当n阶简单无向图为完全图时,任意节点都与其余n-1个节点邻接,边的数量最多,为 n(n-1)/2。因此,当n=20时,边数最多为190;每个顶点都与其余顶点邻接,所有顶点的度数都是19。
-
Q: A total of 7 people took part in the banquet and a friendly handshake took place among the participants. The number of hands-on handshakes known to each of them is:
3, 1, 2, 2, 3, 1, 2
How many handshakes have occurred at the banquet?
某宴会一共有7个人参加,与会者之间进行了亲切的握手。已知他们中的每个人进行握手的次数分别为:
3, 1, 2, 2, 3, 1, 2
请问宴会上总共发生了多少次握手?
In the long history of humanity, everyone may have to shake hands with other people. If someone makes an odd number of handshakes in his life, he is called a Class A person, otherwise he is called a Class B person. The number of people of type A since ancient times is: (assuming that humans can only shake hands with humans)
在人类的历史长河中,每个人都可能要与其他人握手。如果某人在他的一生中进行握手的次数为奇数,则称他为A类人,否则称为B类人。试问从古至今A类人的个数是:(假设人类只能和人类握手)
A. Even number 偶数 B. Odd number 奇数
C. Prime number 素数 D. Complete square number 完全平方数
A: 7, A。 (3+1+2+2+3+1+2)/2 = 7。 具体可参考这篇握手定理理解,讲的比较通俗易懂。
-
Q:
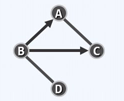
The adjacency matrix of the above digraph is (in order of A, B, C, D) 以上有向图的邻接矩阵为(图中顶点以A、B、C、D为顺序)
A: 画一下就知道了
0 A B C D A 0 0 1 0 B 1 0 1 1 C 1 0 0 0 D 0 1 0 0
搜索树
BST 二叉搜索树
- 中序遍历序列单调非降
- 平均高度
- 随机生成
randomly generated时,平均高度θ(logn) - 随机组成
randomly composed时,平均高度θ(sqrt(n))(根号下n)
- 随机生成
- 查找
- 取决于该节点的深度,或树的高度,O(h)
- 最好:目标出现在树根(或附近),O(1)
- 最坏:BST退化成单链,O(n)
- 插入
- 过程:搜索、插入、更新树高
- 复杂度:同查找,O(h)
- 删除
- 过程:搜索、删除、更新树高
- 复杂度:同查找于插入,O(h)
- 综述:查找、插入、删除等主要操作的效率均线性正比于BST的高度,而在最坏情况下,BST可能退化为列表,效率甚至降至O(n)
AVL树
- 由 G. M. Adelson-Velsky 和 E. M. Landis 于1962年发明,并以他们姓氏首字母命名
- 理想平衡:完全二叉树,过于苛刻
- 适度平衡:树高渐进地不超过O(logn)
- 查找:O(logn)
- 各节点平衡因子的绝对值均不超过1
- 高度为h的AVL树至少包含fib(h+3)-1个节点;包含n个节点的AVL树的高度应为O(logn)
- 失衡节点集:因节点x的插入或删除而暂时失衡的节点,构成失衡节点集,记作UT(x)
- 插入
- UT(x)可能包含多个节点
- 恢复平衡仅需不超过两次旋转,O(1)
- 复杂度:按照BST常规插入算法,需O(logn);复衡需O(1);整体为O(logn)
- 删除
- UT(x)仅含单个节点
- 恢复平衡可能需要O(h)次上溯,因此为O(logn)
- 复杂度:删除需先查找,O(logn);复衡需O(logn);整体O(logn)
Splay Tree 伸展树
- 是平衡二叉树,但无需时刻严格保持平衡
- 最坏情况复杂度与BST/AVL等相同Ω(n),但分摊意义下在O(logn)以内
- 双层伸展
- 将被访问节点伸展至树根
- 使对应分支的长度以大致折半的速度收缩
- 不能杜绝最坏情况(访问最底层节点),但可以有效控制最坏情况发生的频率,从而在分摊意义下保证整体的高效率:O(logn)
B-树
- 由 R. Bayer 和 E. McCreight 于1970年合作发明(为毛不叫
BM Tree…) - 多路搜索树(
multi-way search tree),充分利用内存的高速度与外存的大容量 - 多路平衡
- 所有外部节点深度相等
- m阶B-树(m>=2),设s=(m/2)的上整,每个内部节点有[s, m]个分支,[s-1, m-1]个关键码
- 高度h=θ(log(m, N)),N为关键码总数
- 复杂度:查找、插入、删除均为O(log(m, N)),虽然没有渐进意义上的改进,但耗时的I/O操作的次数已经大致缩减为原先的1/log(2,m)。
RBTree 红黑树
- 每次插入或删除操作后的重平衡过程中,全树拓扑结构的更新仅涉及常数个节点
- 进一步放宽“适度平衡”的标准:任一节点左右子树的高度,相差不得超过两倍
- 红黑树的节点满足以下条件
- 树根始终为黑色
- 外部节点均为黑色
- 其余节点若为红色,则其孩子节点必为黑色
- 从任一外部节点到根节点的沿途,黑节点的数目相等
- 适当转换后,红黑树与4阶B-树等价
- 高度:可以控制在最小高度(完全二叉树高度O(logn))的两倍以内,且从渐进的角度看仍是O(logn),保证了适度平衡
- 查找:红黑树基于BST,O(logn)
- 插入:O(logn)
- 删除:O(logn)
Quiz
-
What’s the worst-case time complexity for searching in a BST with n nodes? 在含n个节点的BST中进行查找的最坏时间复杂度为:
A. O(1); B. O(log2(n)); C. O(n); D. O(nlog2(n));
最坏情况就是退化成单链的情况,此时查找的复杂度为O(n)。
-
Consider inserting a target element e into a BST. when it fails to be found during the search, which node does _hot correspond to? 对BST进行插入操作,对待插入的目标元素e进行查找后,若查找失败,_hot指向的节点为:
A. The node to be inserted 待插入的节点; B. The parent of e after the insertion e被插入后的父亲; C. The left-child of e after the insertion e被插入后的左孩子; D. The root 根节点
看代码:
static NodePtr& searchIn(NodePtr& v, const T& e, NodePtr & hot) { if (!v || (e == v->data_)) { return v; } hot = v; return searchIn(((e < v->data_) ? v->lChild_ : v->rChild_), e, hot); } //! 查找 virtual NodePtr& search(const T& e) { return searchIn(this->root_, e, hot_ = nullptr); }语义约定:
若查找成功,
searchIn()及search()的返回值指向一个关键码为e且真实存在的节点;若查找失败,则返回的数值虽然为nullptr,但它是一个引用,指向最后一次试图转向的节点(可以用作插入)。 在整个查找过程中,hot变量始终指向当前节点的父亲。因此算法返回时,_hot亦将统一指向“命中节点”的父亲。因此对于本题,答案应为B。
-
When atempting to delete a node v of degree 2, what’s the actual node being deleted? 当欲删除的节点v在BST中的度为2时,实际被删除的节点为:
A. v’s direct predecessor in the in-order sequence v在中序遍历下的直接前驱; B. v’s direct successor in the pre-order sequence v在先序遍历下的直接后继; C. the last node in the left branch of v’s right sub-tree v的右子树中左侧分支的最后一个节点; D. v’s parent v的父亲;
节点v的度为2,即有两条边,分3种情况:
- 节点v不是根节点,有一个父亲一个右孩子
- 节点v不是根节点,有一个父亲一个左孩子
- 节点v为根节点,有两个孩子
继续看代码:
static NodePtr removeAt(NodePtr& x, NodePtr& hot) { NodePtr w = x; // 实际被摘除的节点,初值同x NodePtr succ = nullptr; // 实际被摘除的节点的接替者 if (!x->lChild) { // 左子树为空 succ = x = x->rChild_; // 接替者为其右子树(可能为空) } else if (!x->rChild) { // 右子树为空 succ = x = x->lChild_; // 接替者为其左孩子(可能为空) } else { // 左右子树并存的情况 w = w->succ(); std::swap(x->data_, w->data_); // 令x与其后继w互换数据 auto u = w->parent_; (u == x ? u->rChild_ : u->lChild_) = succ = w->rChild_; } hot = w->parent_; // 记录实际被删除节点父亲 if (succ) { succ->parent_ = hot; } // 将被删除节点的接替者与hot相联 // todo 释放被摘除的节点 release(w->data); release(w); return succ; // 返回接替者 } //! 删除 virtual bool remove(const T& e) { auto& x = search(e); if (!x) { return false; } removeAt(x, hot_); this->size_--; updateHeightAbove(x); return true; }对于情况1和2,实际被删除的都是自身,注意参数x为引用类型,因此语义为将被摘除节点替换为其孩子节点。 对于情况3,删除的是v的右子树中左侧分支的最后一个节点。
这道题有点疑惑,按道理,对于情况1和2,并不能选C,但正确答案就是C,难道题目中的度数指的是出度?
-
What is the maximum number of imbalanced nodes after inserting a node in an AVL tree? 在AVL树中刚插入一个节点后失衡节点个数最多为
O(lgn)
What is the maximum number of imbalanced nodes after deleting a node in an AVL tree? 在AVL树中刚删除一个节点后失衡节点个数最多为
O(1)
-
What’s the number of distinct BSTs containing nodes {1, 2, 3 ,4}? 包含节点{1,2,3,4}的不同二叉搜索树有多少棵?(Hint 提示:recursion 递归)
设 f(n) 为 n 个互不相同的节点组成的、拓扑互异的 BST 数量。则:
明显 f(1) = 1;
n=2时, 分别选取两个节点作为树根,由于 BST 需满足中序遍历有序的特性,有两种,即 f(2) = f(1) + f(1);
n=3时,分别选取最小和最大的两个节点作为树根,各有 f(2) 种;选取中间节点作为树根时,分别考虑左子树和右子树的所有情况,显然都是 f(1);即 f(3) = f(2) * 2 + f(1) * f(1);
n=4时,分别选取4个节点作为根节点,则 f(4) = f(3) + f(1) * f(2) + f(2) * f(1) + f(3);
n=5时,分别选取5个节点作为根节点,则 f(5) = f(4) + f(1) * f(3) + f(2) * f(2) + f(3) * f(1) + f(4);
…
类推,得到 f(n) = f(n-1) + f(1) * f(n-2) + … + f(n-2) * f(1) + f(n-1);
f(4) = 14;